
#Bragg condition for diffraction of a wave of wave vector k full#
This shows that the reflected intensity is proportional to the thickness or volume of the crystal, - a result that is true only as long as the crystal is so thin that the reflection leaves the incident, and transmitted, ray at practically its full strength. With the width of the principal maximum given above, the total reflected intensity is then proportional to 2N tan θ n. Since the amplitude maximum is proportional to N+1, or essentially to N if this is large, the maximum intensity is proportional to N 2. The total reflected intensity in any order of reflection is proportional to the area under the principal maximum of the intensity curve. The thinner the crystal, the wider is the angular range of the principal maximum, and the poorer is the resolving power of the crystal as an optical instrument for distinguishing between neighbouring wave-lengths in spectroscopy. The finite angular width of the Bragg reflection is a consequence of the limitation of thickness of the crystal to Nd. Amplitude and intensity curve of the wave reflected by a set of N atomic planes in the neighbourhood of the Bragg angle. The principal or zero order maximum lies between the zeros for s = ☑ and has therefore a width of (2 tan θ n)/N.įig. If we plot the reflected amplitudes as a function of the difference of the angles of incidence and reflection from the Bragg angle, φ = θ - θ n, each Bragg angle is seen surrounded by zeros of the reflected amplitude and corresponding zeros of intensity obtained by squaring the curve. Or, since the difference of angles is usually very small, this can be approximated by
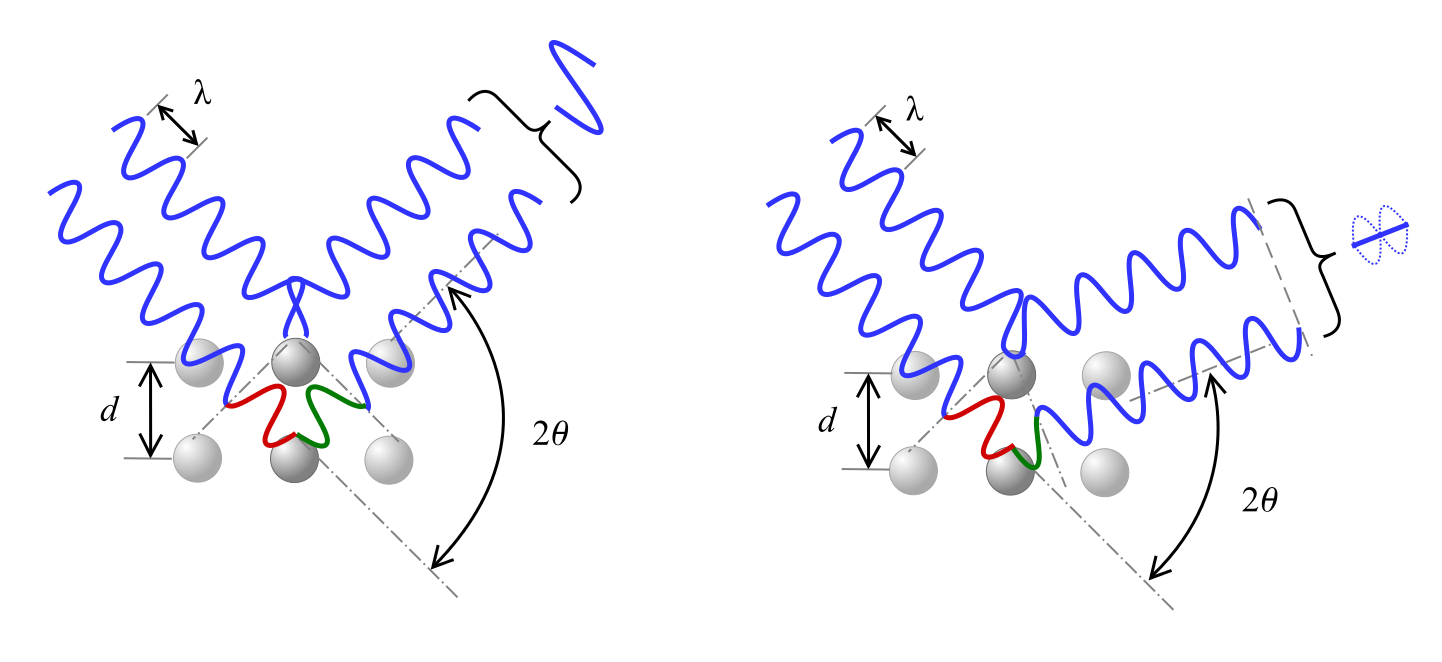
The condition for the angles under which these 'secondary zeros' of the reflection curve occur isĪnd the angular distance of the sth zero from the Bragg angle θ n is given by For then there will be for any reflected elementary wave one of opposite phase superimposed. Their effect cancels out to optical field zero if the maximum phase difference throughout the crystal corresponds to an entire wave-length path difference, or, indeed, to any multiple of it, say sλ, where s is an integer. By putting together the information on various sets of reflecting planes, obtained in this way with the X-ray spectrometer, the first crystal structure determinations were made.Īs the angle of incidence is slightly varied from the Bragg angle, a phase difference develops between reflections from neighbouring planes and re-inforcement of the reflected waves becomes less perfect. If λ is known and θ n measured, then the value of n/d follows, and if the order can be found, the value of the spacing of the set of reflecting planes is determined. The greater the wave-length, the larger the glancing angle for reflection on the same plane the greater the spacing, the smaller is the glancing angle for a given wave-length. order reflections occur, for n = 1, 2, 3. This 'Bragg Equation' determines the angles θ n under which the first, second, third. Therefore maximum amplitude of the reflected wave is obtained for angles θ n such that If this equals a whole number, n, of wave-lengths λ, then the phase difference is zero throughout the crystal. The path difference between reflections on neighbouring planes is 2d sin θ. Now the difference of optical path for the top and bottom wave is shown by the heavy-drawn path lying between two parts of the wave-fronts of the incident and reflected waves. Bragg reflection on a set of N atomic planes. Should all waves arrive in the same phase, then full re-inforcement of the waves takes place to an amplitude of N+1 times that of the single reflected wave.įig. If, however, the phases of all the reflected waves arrive within less than one half wave-length phase difference, then all reflected amplitudes will build up together to an optical field in the direction of reflection, without any actual cancellations of contributions. There exists, then, only the transmitted wave. Under most angles of incidence, θ, the waves reflected from neighbouring planes will show a phase difference, and where all the reflected waves come together at great distance from the crystal, the superposition of these waves of systematically increasing phases will lead to a cancellation of amplitudes and to optical field zero. It is assumed that each atomic plane reflects a very small fraction of the incident amplitude, small enough so that the weakening effect of this reflection on the incident amplitude may be neglected throughout the crystal. BraggĬonsider a set of N+1 equidistant atomic planes of spacing d, and a monochromatic plane X-wave falling on it at a glancing angle θ (Fig.


 0 kommentar(er)
0 kommentar(er)
